CS190N Numb3rs -- Sacrifice

The situation:

Charlie is able to observe, through the miracle of "van Eck phreaking," the rhythm of the keystrokes used by a killer to login to his victim's computer and subsequently erase the data from its hard drive (see those 0s and 1s on the screen?). By matching this rhythm with the password-entry rhythms of a known user, he is able to identify that user as the killer. How did he do it? What do those horizontal bars mean? Will it hold up in court? Most importantly, after Don clearly understood what Charlie was talking about, why did Charlie feel compelled to launch into that whole thing about concert pianists? Stay tuned for the answers to precisely none of the above questions; instead, we will take a look at some better questions, their answers, and a lot of information about information.

Speaking Hypothetically

In the first unit, we encountered the notion of a confidence region as a means of quantifying the information obtained through a random sample. In fact, there is another concept in statistical inference that is related and equally important as, but distinct from, the confidence region &mdash the Castor to its Pollux if I may, the Mary Kate to its Ashley if you will &mdash namely, the hypothesis test. As my beloved audience seems to have encountered ideas in this space before, I will give a brief but meaningful resumé of the simplest examples of these things.

Hypothesis tests differ from confidence regions in their goals: Rather than trying to estimate a parameter, with some measure of certainty, a test attempts to answer a yes-no question, again with a measure, quantified in a very specific way, about the certainty of the answer. The question typically involves the equality of a population parameter, such as the mean, either to a constant or to the corresponding parameter of a second population. For example, we may wish to test whether the mean height of all male UCSB students is 5′10″, based on a sample, or we may wish to test whether there are differences in the mean response of patients to two different drugs. I could go on all day with examples of how statistical tests can be used in the real world.

The most straightforward examples of hypothesis tests involve the question of whether a population mean is equal to a given constant &mu0. The statement that they are equal is called the null hypothesis and is written out formally like so:

H0:  &mu = &mu0

(H0 is pronounced "aitch null.") Against the null hypothesis, we present an alternative hypothesis, written Ha, which in this example can take one of three forms, depending on what specific question we're interested in answering:

Ha:   &mu &ne &mu0  or
&mu < &mu0  or
&mu > &mu0

(For the sake of simplicity, let's continue the present discussion assuming that the alternative hypothesis of interest is the "&ne" version.) Having set up our opposing hypotheses, we then move along to taking a sample and evaluate, in a way that will be discussed in our usual painful detail below, the two hypotheses relative to the data.

Note the asymmetry in the two hypotheses: they are not interchangeable. Our null hypothesis &mdash and this is absolutely typical of null hypotheses in general &mdash is too specific to be literally true. I mean, if we return back to the example of the UCSB males, it's pretty clear that if we had enough precision in our measuring instruments and used this precision in recording our measurements, the mean height would have (essentially) no chance of being exactly 5′10″. So what's all this hypothesis-testing business about, anyway? Why couldn't we just answer any null hypothesis involving an "equal" sign with "Uh, no, like, what are the chances? Please!" before even taking a sample, and then spending all the time and grant money we saved on a really good sandwich?

The fact of the matter is that you can ask, and answer, many interesting questions that don't involve the numerical precision of the null hypothesis. Often, for instance, the null hypothesis is something we posit skeptically, defying the sample to provide really good evidence against it. I'll give you an example: Suppose that we know from a bunch of evidence that the average cold sufferer takes just about 4 days to get over the cold. Little Giant Pharmaceuticals releases a product that it claims will reduce the amount of recovery time. Let's posit that their product had no effect and consider the times-to-recovery from a cold as our population. We set up the null hypothesis H0:  &mu = 4 and sit back and wait for the (sample-based) evidence. Now, if they were to come back and say, "We gave it to three cold sufferers and, on average, they took only 3.6 days to get over their colds!" we would have cause to doubt whether the product made any difference at all; in other words, that kind of data is not all that out of whack from our assumed value of 4 for the mean. On the other hand, if they did a responsible clinical trial and found that, among 472 cold sufferers, the mean time to recovery was 1.9 days, well, we might sit up and take notice. All this even though, really, what are the chances in either case that the mean time to recovery for people receiving the treatment was exactly 4 days &mdash or even exactly equal to the mean for the population at large? Nil, that's what they are. Heck, how can we even know the mean for the population at large in a situation like this one? And yet we still might like to use the data in order to say something meaningful about the impact of the treatment on the duration of colds.

What's going on is that, just as we state the two hypotheses in an inherently asymmetric way, we also treat them asymmetrically. It's kind of skepticism vs. cynicism: The null hypothesis is set up to assume skeptically that there is "no difference," "no change," "no effect," and is what we will assume to be true unless the sample data provide convincing (this notion of "convincing" is adjustable, as we'll see) evidence that it is false. This evidence will come in the form of an analysis of how likely it would be to gather the evidence we did, cynically assuming H0 to be true.

Now we're beginning to see how the details of a hypothesis test look. Let's go through a specific example to see all the moving parts:

Example: Suppose that it is known that all college-age males in the country have a mean height of 5′10″ with a standard deviation of 2&Prime. You wonder whether there's any difference in mean height between male UCSB students and those in the rest of the country. Let's suppose for simplicity's sake that you are happy to assume that the UCSB students' heights are normally distributed with unknown mean &mu but with known standard deviation &sigma = 2. Your hypotheses are then

H0:   &mu = 70
Ha:   &mu &ne 70

and off you go to find yourself a random sample. You measure the heights of 16 students and find that their mean height was 70.9 inches. What do you make of this data? 70.9 is different from 70, but on the other hand it's not different by a huge amount, but on the other other hand the mean of a decent-sized sample should be pretty darn close to the population mean, but on the other other other hand is 16 big "decent-sized"? is 0.9 not "pretty darn close"? Before we run out of hands, let's do some math, shall we? Given our assumptions, and assuming that H0 is true, the sample means for random samples of size 16 should be normally distributed with mean 70 and standard deviation 2⁄√16 = 0.5. Under this set of assumptions, then, our particular sample mean lives here in the distribution of all possible sample means:

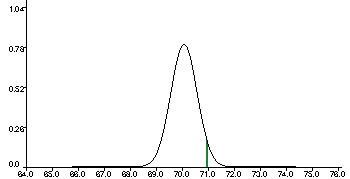
To understand how "unusual" this sample is, we should look at the probability that a sample mean would be at least that far away from the true mean (assuming, all along, that H0 is true). That's the white region in the graph below &mdash sorry, I couldn't figure out how to make the applet I scared up reverse the colors &mdash and is called the p-value associated to this sample for this test.

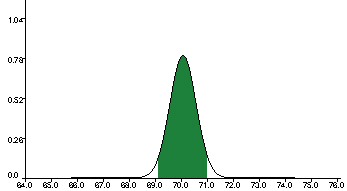
The white represents the region at least 1.8 standard deviations away from the mean. How much white area is there? Here is the least annoying normal table I could find in 30 seconds of online hunting about; it shows that .0359 of the population lives at least 1.8 standard deviations to the right of the mean, and an equal amount lives at least 1.8 to the left, so all told, about 7.18% of the population is in the white zone &mdash, that is, the p-value in this case is p &asymp .0718. This means that, assuming for the moment that the mean really is 70, if you took a bunch of random samples of size 16, about 7.2%, or about 1 in 14, would have a sample mean at least as far away from 70 as this one is. What does this tell us about the population mean?

This brings us to the concept of significance. Besides setting up our hypotheses, we need to decide, before taking our sample, how small the p-value, which represents that "outside" fraction of the population needs to be before we'll go ahead and reject H0 in favor of Ha. This threshold is called the significance level of the test, denoted by &alpha. In other words, we say ahead of time, "We'll take a sample, measure its p-value, and reject the null hypothesis if p < &alpha." I hope it's clear by how things are set up that the smaller &alpha is, the more certain we need to be that the the null hypothesis is incorrect before rejecting it: The significance level &alpha represents the fraction of the time that you are willing to reject H0 incorrectly. You realize, of course, that it's folly to say, "Hey, I never want to reject H0 incorrectly!" The only way to be sure you'll never reject it incorrectly is never to reject it, and that isn't a very productive use of your data. A standard value for significance is &alpha = .05, just as 95% is standard for a confidence interval. Note how much this privileges the null hypothesis: We don't want to reject it unless we see evidence extreme enough to be in the rarest 5% if it were true. Also note that lower values of α, while they make it less likely that you reject a true null hypothesis, they also make it more difficult to reject a null hypothesis that is substantially false. Bearing this tradeoff in mind, and analogously again to the situation we encountered with confidence intervals, we can use various values of &alpha, depending on what we need to accomplish, the real-life consequences of rejecting a true H0, and the consequences of retaining a null hypothesis that does not accurately model reality. In the current example, if we have proposed &alpha = .05 for the significance level of interest, then we cannot reject the null hypothesis, because the p-value .0718 is larger than &alpha. On the other hand, we could reject the null hypothesis at a significance level of .1.

There are a couple of other parallels between significance and confidence that we ought to recognize. First, significance, like confidence, is similar in form to probability, but it is not probability! For instance, it makes no sense in this example to say "There's a 7.2% probability that H0 is true." H0 is not a random event &mdash it's either true or it's false, and no random sample can change which of those it is. Second, level of significance has a direct relationship with confidence level, at least in this simple example. Namely, for a given sample we reject H0 in favor of a two-sided alternative at significance level &alpha precisely when the proposed mean &mu0 lies outside the (1−&alpha) confidence interval for the mean produced by our sample. Another nifty way of saying the same thing is that a level-C confidence interval consists of all the null hypothesis values that you can't reject at significance level (1−C).

Let's talk for a moment about the other two possibilities for Ha, the so-called one-sided alternatives. Such an alternative could have arisen in this example with a very small change in wording: Suppose that instead of wondering whether the average UCSB male student is different from the national average, you wondered whether the average UCSB student is taller than the national average. Our alternative hypothesis would become

Ha:   &mu > 70,

and in order to answer the question we're asking, we need to measure how unusually large our sample mean is: We would clearly never reject the null in favor of the alternative if we got a sample mean that was way below 70. For the specific situation we set up, with a sample size of 16 and sample mean of 70.9, the p-value is the probability of seeing a sample mean that large or larger when H0 is true, is only .0359, so we can reject the null hypothesis in favor of the alternative at the &alpha=.05 level. In general, only those outcomes supporting the alternative hypothesis can contribute to the p-value.

There is a connection to confidence intervals with one-sided test as well, but this time the interval is infinite on one side, and rejection of the null at significance level &alpha happens when the mean proposed in H0 lies outside the (1−&alpha) lower (as in our case) or upper confidence bound for the mean.

A tidy way to do the calculations is to identify the test statistic, in this case the normalized z-value, under H0, of the sample mean, namely (X &minus &mu0)⁄(σ⁄√n) and to determine whether this test statistic exceeds (positively or negatively or either one, depending on the nature of the alternative hypothesis) the critical value for the test at the significance level chosen.


The above example, while it's a little bit simplified, contains most of the ingredients to the usual normality-based approach to hypothesis testing. Now, let's have a careful look at the problem we're actually trying to solve. When you did your typing assignments, we measured the time intervals between each pair of keystrokes and gathered data about particular letter combinations. For example, in the Marhta Stewart article there are a lot of "th" strings, so we now have pretty good information on the speed at which each of you (who completed the assignment) tends to type "th." We propose to use data like this in order to ascertain whether two samples were typed by the same person. Can we set this up as a hypothesis test? We might hope to distinguish two typists merely by the mean speed with which they type their various letter combinations. Suppose then that we're given two typing samples, which I will label with the very imaginative scheme Sample 1 and Sample 2. The null hypothesis of "no difference" would look a little like

&muaa,1=&muaa,2
&muab,1=&muab,2
.
.
.
&muzz,1=&muzz,2

in other words, the mean values for each sequential letter combination are equal between the two "populations" from which the samples were drawn; the alternative would simply be that the null is false, since even one mean that was truly different would indicate two different typists. In the best possible case, we would be able to reject the null hypothesis when the samples came from different typists and would retain it whenever they came from the same typist. (In theory, there are 676 equations describing the null hypothesis if we limit ourselves only to combinations of small letters! In practice, of course, things like "qp" and "jb" don't occur, and combinatins such as "bv" are pretty rare.)

I hope that it's clear that this particular hypothetical hypothesis test differs in substantial ways from the above example. First of all, we have no precise knowledge about any of the standard deviations. Thus, even a stripped-down version of the above in which we examine the mean speed for a single keystroke pair of a single typist against a specific value, say 300 milliseconds, so that our hypotheses are

H0:  &muth = 300
Ha:  &muth &ne 300

already represents a departure from what we discussed. The extra complication is not huge, however, provided that our data looks reasonably normal or we have a sample size that's big enough (30 or so). Just as in the case of confidence intervals, the process is very similar to that for the problem with known variance, except that the standard deviation &sigma needs to be estimated by the sample standard deviation s, as we calculated it way back in the here, with (n−1) degrees of freedom, where, as usual, n is the sample size.

The next departure is that we really want to compare the means from different samples to each other rather than comparing the mean from a single sample to a constant. This is also a very natural thing to do that has all kinds of real-world instantiations: for example, a researcher may wish to see whether a particular drug lowers blood cholesterol, on average, more than a placebo or than some existing treatment. To look at another simplified version of our problem, suppose that we want to see whether the "th" speeds of the typist(s) from which two samples come are different. We would then set up the hypotheses

H0:  &muth,1 = &muth,2
Ha:  &muth,1 &ne &muth,2

As usual, we make the formal assumption that both populations are normally distributed, with the usual observation that this assumption becomes less important with larger samples, and if we also make the assumption that the standard deviations of the populations are equal, then the test statistic looks like

x1 &minus x2
√[(n1s12 + n2s22)&frasl(n1 + n2 − 2) &sdot (1&frasln1 + 1&frasln2)]

(that radical sign covers the entire denominator!), and the critical value is taken from a t-distribution with (n1 + n2 &minus 2) degrees of freedom. (In the above formula, all the means, standard deviations, and sample sizes come from the "th" values of the appropriately subscripted typist.)

Let's examine the test statistic for a minute. The numerator is not too unexpected: you'd want it to depend in a very direct way on how different the two sample means are. The first factor in the denominator is a weighted average of the variances, and the second factor reflects the idea that sample variance decreases as the square root of the sample size.

In fact, the above method is very sensitive to the assumption that the standard deviations are equal. Unlike most assumptions about distribution in this space, it's not enough to size up the two samples and say, "Yeah, the spread looks just about the same." You should have a good reason to believe ahead of time that the two populations have the same standard deviation before you undertake a test using this method; if they do not, in particular, there is a real chance that your significance level is not accurate, meaning that you would incorrectly reject the null hypothesis the wrong fraction of the time. If you don't have a good reason to believe that the standard deviations are equal, instead use the test statistic

x1 &minus x2
&radic(s12⁄n1 + s22⁄n2)

against a critical value from the t-distribution with min(n1, n2) degrees of freedom. Many authors advise us to stay away from the previous test entirely and always use this one, due to its aforementioned sensitivity to the assumptions. The drawback to this test is that it is more conservative than the previous one, in the sense that it rejects the null hypothesis less often: Even though the test statistic is a tad bigger, the number of degrees of freedom is much smaller, so the critical value is correspondingly quite a bit larger. (If that business about degrees of freedom doesn't make sense, stare at that t-table to which I linked you above and think about what t-distributions are all about.)

Well, this still doesn't quite give us a method for attacking the problem posed, but we're getting there. One method that might look attractive on the surface goes a little like this: Let's do t-tests for each letter pair separately, rejecting that big null hypothesis if we reject any of the simple ones. A minute's reflection will show, I believe, that this won't quite work. Let's suppose that we choose &alpha = .05 as our significance level, and let's suppose that there are 100 letter pairs that actually occur in the typing samples. Since each individual t-test has a 5% chance of rejecting a true null hypothesis, and we're doing 100 such tests, we're almost certain to reject our H0, even if it's true! (In fact, the probability of rejecting a true null can be calculated in the usual way &mdash I hope you could all reproduce this if you had to &mdash as 1 &minus .95100 &asymp .996.) We'll speak later of ways to improve this general approach to the problem. Meanwhile, let's look at a couple of other common tests and how they relate to our problem.

Chi-square (&chi2) test  You (may) have actually seen a test for carrying out multiple comparisons similar to the ones we see here, namely the &chi2 test for equal distributions of categorical data. It's actually possible to extend the &chi2 test to continuous data. One does this by (somewhat arbitrarily) making bins comprising ranges of the data and then, for each measurement, converting its numerical value into the label of the bin into which it would fall. In our situation, we might take all of the keystroke pairs in consideration between two typing samples, pool all of the measurements together, order them, and break the range of measurements into five bins, labeled A through E, with 20% of the data in each bin. We could then make counts of how many of each keystroke pair for each typist fell into each of the bins, obtaining counts caaA,1, caa,A,2, caa,B,1, ... Our null hypothesis should express that the proportions of the keystroke pairs over the bins are independent of the typist who produced them; in short (sort of)

H0:   The compound variable (keystroke pair, bin) is independent of the typist variable.
Ha:   H0 is false.

To test this, one forms a contingency table, which in this case would be very tall and thin:

caa,A,1caa,A,2
caa,B,1caa,B,2
.
.
.		.
.
.
czz,E,1czz,E,2

For contingency tables such as this one, it is of interest to form the marginal totals for each row, written ci+ = &sumj cij, and for each column, namely c+j = &sumi cij. If the variables were independent, then the proportion of things in the i, j cell, which is equal to cij ⁄n (where n is the total number of things in all the cells) should be equal to the proportion in the ith row times the proportion in the jth column, that is, ci+ ⁄n &sdot c+j ⁄n. This says that cij should be about equal to ci+ c+j ⁄n. Accordingly, we call this last value the expected count for cell (i, j); note that the expected count for a cell need not be an integer! Our test statistic measures how far off this is from being true; since errors in either direction are evidence for our alternative against our null, it's fairly natural to imagine that they'd be squared values; also, the differences should be measured relative to how big we expect them to be; for example, if your expected cell count is 400 and there are 390 in that cell, that's probably not as big a deal as expecting 15 and seeing 5. Bearing all this in mind, I hope you're not too surprised at the form of our test statistic:

&chi2 = &sum&sumi, j [cij &minus (ci+ c+j ⁄n)]2
ci+ c+j ⁄n

Believe it or not, under H0, the statistic &chi2 has asymptotic distribution &chi2, with degrees of freedom equal to (# of rows &minus 1)⋅(# of columns &minus 1). In our case, this would be 675, at least in principle. As a practical matter, the asymptotic distribution is pretty good, as long as there are relatively few cells with low expected counts. The rule of thumb I've seen is that no cell should have expected count less than 1 and that fewer than 20% should have expected counts less than 5. Observe that for the problem we're looking at, we have some control over these considerations: if either of the above conditions on expected counts is violated, we can reduce the number of bins into which we throw our keystroke pairs; we can also reduce the number of keystroke pairs we consider, which we'd probably end up doing for any test! The real drawback to the &chi2 test is philosophical: By lumping numerical data into bins, we have destroyed a lot of information that is potentially useful; additionally, &chi2 treats the bins simply as categories and even "forgets" which bins correspond to larger numbers than which others. Generally, &chi2 should not be your first choice when looking at numerical data.

ANOVA F-test   What our problem is really looking to do is to compare multiple means, and a common test that does, in fact, compare multiple means is the so-called analysis of variance, or ANOVA for short. Superficially, then, I think our problem looks more like an ANOVA problem than like any of the other models we've discussed above. The idea of ANOVA is that, given a number of discrete categories, numbered 1 up to k, and numerical data xij in each category i, one can try to determine whether the populations within the categories all have the same mean by breaking down the total variation within the sample into the variation within the categories and the variation between the categories. Intuitively, if the variation between categories is much larger than the variation within them, we would seem to have reasonable grounds to believe that the means are not all the same. Under the assumption that the data in each category is normally distributed (becomes less important with increasing sample size) and has about the same standard deviation (remains important!!), we can form the hypotheses

H0:   &mu1 = &mu2 = &sdot&sdot&sdot = &muk
Ha:   H0 is false.

The analysis of variance goes like this: Measure some sort of notion of "typical" squared deviation from the mean within the categories as s&tilde2 = 1&frasln &sum&sumi, j (xij &minus xi)2, and measure the overall variance of the sample as s&tilde02 = 1&frasln &sum&sumi, j(xij &minus x)2. Note that the difference between these statistics is that s&tilde2 uses the sample mean within the appropriate category in each term, while s&tilde02, representing the null hypothesis, uses the overall sample mean for every term. One can show that under H0, the test statistic
F=
(s&tilde02 &minus s&tilde2)⁄k &minus 1
s&tilde2⁄n &minus k

has an F-distribution (remember those?!?) with (k &minus 1, n &minus k) degrees of freedom.

Unfortunately, a moment's inspection into what this test does shows that it cuts the data in the wrong direction, so to speak. For instance, we could use ANOVA to figure out whether there were significant differences among the "th" keystroke-pair speeds for a number of different typists, and it could also be used to measure whether there are significant differences in the speed with which a single typist types a number of different keystroke pairs. Without further enhancement, however, it's hard to see how to use ANOVA for our problem.

What do all these tests have in common, how are they constructed and how does one construct similar tests to perform one's own particular bidding?

A Likelihood Story

In order to understand this, we need to understand the concept of likelihood. The big idea is to get a handle on how well a probability model "explains" a random sample. I hope you're still smarting from my last diatribe about how population characteristics are not random and we therefore cannot speak of the probability that a population parameter has a certain value. Likelihood is a way of getting around that, in our favorite tail-wagging-the-dog sense.

Suppose that we've decided that our population is distributed according to some specific family (for example, normal), but one or more of the parameters is unknown. Given a random sample, the likelihood associated to a choice of parameters is just the product of the probabilities of the sample elements in the case of discrete distributions and the product of the values of the density functions at the sample elements in the case of continuous distributions. The likelihood function is thus a function of the parameter(s), given some sample data, while the probability or probabiliy density function is a function of the value that the variable can take on, but they're the same function! I'll call probability or density functions ƒ(x), typically, and likelihood functions L, or L(&theta), or even L(&theta | S) if I want to emphasize the sample S on which I based the likelihood calculation.

Let's do a fairly simple example. Suppose we have a coin with p = P(heads) unknown. We toss the coin four times, and our sample S consists of three heads and one tail. The value of .5 for p has likelihood L(.5) = .54 = .0625, while L(.8) = .83 &sdot .2 = .1024.

For a given sample, given two choices of parameter values, the one with a higher likelihood is the one gives a higher probability that the sample would have occurred if it were the true parameter, and it's generally accepted that parameters of higher likelihood are therefore "better" at explaining the sample. Thus, in the above example, we would prefer p = .8 over p = .5 as a model for the coin. (If this doesn't sit well with you, I don't blame you; see the following Bayes' Rule discussion.) Please note here that we really can't attach too much meaning to the value of the likelihood function for a specific value of a parameter, only its value relative to those for other values of the parameter. In fact, two likelihoods can be compared directly according to their ratio, due to considerations based on Bayes' rule (again see the section below for details).

We can also calculate likelihoods for continuous distributions, such as the normal. For continuous distributions, of course, you need to replace probability of an outcome with probability density at that outcome. If this makes you a little nervous, imagine attaching a little bit of width &Deltax onto each of the outcomes in the sample, so that we're talking about the honest-to-goodness probability of falling between xi and xi + &Deltax for each element xi in the sample. If &Deltax is small enough, this probability is approximated well by ƒ(xi)&Deltax; in comparing the likelihood functions for two different values of the parameter, you would have exactly the same number of factors of &Deltax in each calculation, so the question of which one was bigger, and in fact their ratio, would only depend on the densities.

When you're looking for a meaningful estimate for a parameter based on a sample, the maximum likelihood estimator (MLE) has a number of attractive features. First of all, ure and simple, in terms of likelihood functions, it's the best one at explaining the data, in the sense that there is no other value for the parameter for which the data would have been more probable. In addition, MLEs have good properties relative to the notion of efficiency, which is a bit complicated for the scope of our little class, but essentially, MLEs tend to be the "best" estimator possible in terms of mean square error from the parameter that they are estimating.

Let's do a couple of sample calculations of MLEs. First, suppose we toss a coin with unknown p = P(heads) n times, and we toss k heads and (n &minus k) tails. Then the likelihood function L(p) = pk (1−p)n−k. To find the MLE for p, denoted by p^ (that ^ is supposed to be on top of the p! I love HTML!!), we need to maximize L, which is certainly a nice differentiable function of p between 0 and 1. It's also easy to calculate L(0) = 0 and L(1) = 0 (unless k = 0 or k = n; these cases we'll handle in a minute), and L is a nonnegative function by its very definition, so it has a max in there somewhere! We'll find it using calculus. First, note that since the logarithm function is monotone increasing, the value of p that maximizes log(L) is the same value that maximizes L, and log(L) is easier to handle. We calculate

log(L(p)) = k log(p) + (n−k) log(1−p), so

d⁄dp (log L(p)) = k⁄p &minus (n−k)⁄(1−p).

To find the maximum value, we set this derivative equal to 0. When we clear denominators we find that k(1−p) = p(n−k), so k−kp = np−kp, and thus p^ = k⁄n. I hope you agree that this makes intuitive sense: our best guess for the probability of heads is the proportion of heads in our sample.

The same result is true in the annoying "corner cases" k = 0 and k = n. In the k = n case, for example, L(p) = pn, which is pretty clearly maximized on the interval [0,1] at p = 1, so p^ = 1, which is still equal to k⁄n! Similarly, if k = 0, p^ = 0 = k⁄n, so we find that the same MLE formula is valid for any sample.

Now let's try one with a continuous distribution. Suppose that we have a random sample from a normal distribution with unknown mean &mu and known standard deviation σ. Let's calculate μ^, the MLE for &mu, from this sample. Recall that the density function for a normal distribution is

ƒ(x) = 1⁄(√2&pi &sigma) e&minus(x−&mu)2⁄ 2&sigma2

so for a given sample S = {x1, x2, ..., xn}, the likelihood function is given as

L(&mu) = &Pii 1⁄√2&pi&sigma e&minus(x−&mu)2⁄2&sigma2.

Clearly the log trick is in order once again! Taking the log turns the product into a sum and gets rid of exponents:

log L(&mu) = &sumi [log(1⁄√2&pi &sigma) + log(e&minus(xi−&mu)2⁄2&sigma2)] = n log(1⁄√2&pi &sigma) &minus &sumi(x−&mu)2⁄2&sigma2,   so

d⁄d&mu (log L(&mu)) = &minus&sumi(xi &minus &mu)&frasl&sigma2  =  (n&mu&minus&sumxi)&frasl&sigma2.

Setting this equal to 0 amounts to setting the numerator equal to 0, and this gives &mu = &sum xi⁄n = x. As this is the only critical point, and you could surely make log L(&mu) as small as you like by making &mu really really big, the critical point must be a maximum, which as we said just 30 seconds ago makes it a max for L itself. So &mu^= x. Again, this result probably isn't too surprising: the most likely choice for the population mean is the sample mean.

We can stretch the above example to find the MLE (&mu, &sigma) for a normal when both parameters are unknown! The likelihood function L(&mu, &sigma) is exactly the same symbolically as we calculated before, but since this time &sigma is a variable, we need to set the two partial derivatives of log L equal to 0 in order to find the max.

Exercise Carry out the calculation for the MLE for (&mu, &sigma). Based on what we've seen from MLEs so far, is your answer just exactly what you had expected?

Bayes' Rule

If you really want to understand likelihood, you need to come to grips with Bayes' rule. I hope you've seen this in probability class, but let's review quickly how it works. Recall that for a given random variable, an event is a subset of the set of all possible outcomes of the variable that has a measurable probability (maybe 0). If A and B denote events, then the probability that both occur, written P(A &cap B), can be expressed as the probability that A occurs times the probability, given that A occurs, that B also occurs. In symbols,

P(A &cap B) = P(A) &sdot P(B | A).

I hope this make intuitive sense: If 30% of all students on campus have "first-year" status, and 10% of all students with "first-year" status are business majors, then the probability that a randomly chosen student will be a first-year business major is .3 &sdot .1 = .03. Note that this example does not assume that being a first-year student and being a business major are independent; thus, if you were only given the overall percentage of business majors on campus, you would not have enough information to do the final calculation.

Since the event A &cap B is surely the same event as B &cap A, we can reverse the roles of the two variables on the right-hand side of the above equation and obtain

P(A) &sdot P(B | A) = P(B) &sdot P(A | B);

Dividing both sides by P(A) then gives Bayes' rule in its simplest form:

P(B | A) = P(B) &sdot P(A | B)⁄P(A).

The way this is generally interpreted is as follows: Regard P(B) as your prior belief about the probability of B, only knowing what you know. Then you get some additional information about the situation, in the form of event A. This changes your perceived probability that B is true, and Bayes' rule tells you exactly how that probability gets changed, provided you're able to calculate everything else.

Bayes' rule often gets used in the following way: B is a statement about a population parameter, and A is the outcome of a random sample. Let's revisit the above example with the coin and P(heads), in a couple of different ways, so we can see in what way that example squares with reality and in what sense it does not.

First, suppose that I have two coins in my pocket. They are indistinguishable in appearance, but one of them is fair, and the other has P(heads) = .8. I pull one of them out of my pocket. At this point, your prior belief about this coin is that there's a probability of .5 that it's the fair coin and .5 that it's the unfair coin. Next, I toss the coin four times, and it comes up heads three times and tails once. Now what is your belief about the coin?

What I'm asking for in symbols is P(unfair | three heads and one tail). My prior P(unfair) is equal to .5, P(three heads and one tail | unfair) = .83 &sdot .2 = .1024. Finally, P(three heads and one tail) = P(three heads and one tail | fair) &sdot P(fair) + P(three heads and one tail | unfair) &sdot P(unfair) = .0625 &sdot .5 + .1024 &sdot .5 = .08245. So by Bayes' rule, P(unfair | three heads and one tail) = P(unfair) &sdot P(three heads and one tail | unfair)⁄P(three heads and one tail) = (.5 &sdot .1024)⁄.07445 &asymp .621. So you are now about 62.1% certain that the coin I pulled is the unfair one, versus 37.9% for the fair coin &mdash a ratio of better than 1.5 to 1. In this case, the ratio of your beliefs coincides with the likelihood ratio, because your priors for the two values were equal, so they would cancel in the ratio, as would the denominators, leaving only the likelihoods.

Now, I pulled a little bit of a fast one there, since, once again, the identity of the coin that was used to produce the sample was not a random event, so I can't really speak of the probability per se that it's fair or unfair &mdash it's either certainly one or certainly the other, regardless of the sample. I finessed that point in my language above by using words like "belief." In point of fact, what we're really talking about here is likelihood. Since likelihood is calculated in the same way that probability is, it obeys the same laws, so in particular Bayes' rule calculations still work for likelihoods. Therefore, in particular, it makes sense to talk about likelihood ratios and, as far as it makes sense to say it, we would say that it's about 1.5 times as likely that it was the coin was the unfair one as it is that it was the fair one.

In fact, the Bayesian philosophy toward statistics is that there is no distinction at all among proability, confidence, significance, and likelihood, because a Bayesian will treat any unknown quantity as a random variable. For the depth into which we will go in this class, the difference between our approach and that of a Bayesian is more or less purely semantic &mdash not to say that the semantics aren't important, but at least the calculations, and conclusions drawn, would be similar in effect.

In contrast with the preceding example, suppose you just find a coin lying around. You're 99% sure this is a fair coin (how do they make unfair coins, anyway??), and you estimate that there is only a .001% chance that P(heads) = .8. (I guess it's more realistic to put a continuous probability distribution on your belief about the true value of P(heads), but that would make the example far more complicated to calculate.) Again, you toss the coin four times, and it comes up heads three times and tails once. Your belief that the coin is fair looks like .99 &sdot .0625⁄P(three heads and one tail). We actually don't have enough information to calculate the denominator, but we can at least calculate the ratio of your beliefs about .5 versus .8. Your belief that the coin has P(heads) = .8 is .00001 &sdot .1024⁄P(three heads and one tail). The ratio of the two beliefs is thus .99 &sdot .0625⁄.00001 &sdot .1024 &asymp 60425. So you're still thinking that it's 60,000 times as likely that the coin is fair as that its P(heads) is .8. I hasten to point out that this is a smaller number than your prior ratio, which was 99,000, but your belief hasn't been shaken all that much.

The moral? If you have prior beliefs about how you think the world is, you need to take those into account when you use statistics to make decisions &mdash otherwise, you go running around thinking that almost every coin you meet is unfair. The typical paradigm for our brand of statistical inference is that the prior is noninformative, meaning that we have no prejudices about what the parameter in question is before we start. In that case, we take the ratio of beliefs to be the likelihood ratio, just as it turned out in the first scenario. In fact, while in general the idea of a noninformative prior is a slippery thing, in the case of a finite distribution a noninformative prior can be expressed as the uniform distribution. If your prior is noninformative, then your best estimate for the parameter is the maximum-likelihood parameter. As the second scenario showed, however, higher likelihood does not always translate into stronger belief when you have informative priors in play.

Likelihood-Ratio Tests

OK, let's put things into perspective for a moment or two, shall we? We looked at a few common significance tests, without really getting into how and why they did the job, and we observed that they seem to fall short of ideal for the problem we're trying to solve. Thus, we see a need to expand our repertoire of significance tests! There's not exactly a "canned" test that is guaranteed to work perfectly, as in the simple cases handled by some of the tests discussed above, so we'd like to devise our own test. And in order to do this, we needed to understand how to devise one's own significance tests. Having reached that point in the intellectual progression, you were kind enough to believe my assertion that we needed to understand likelihood, which I think we now do pretty well. "So," I hear you saying, "WHAT THE HECK DOES THIS HAVE TO DO WITH MAKING TESTS??!" Sheeze. Don't shout.

As we saw in the Likelihood and Bayes' Rule sections, the likelihood ratio is a reasonable way compare different estimators for a parameter (or vector of parameters), which I'll call &theta. By its very definition, the MLE θ^ is going to have the largest likelihood value; for any proposed choice of &theta, the likelihood ratio for a particular proposed value of the parameter with θ^ gives a good measure of how well that θ-value explains the data. Now back to a hypothesis test: Since θ^ comes from a particular sample, it is subject to sampling variability, so we can't reasonably expect that the value &theta0 in H0 will match up precisely with θ^, but on the other hand, if &theta0 does too lousy a job of explaining the data, we'd want to reject H0.

A sensible test, then, is to construct the statistic

&Lambda = L(&theta0)⁄L(θ^) ,

intending to reject H0 if &Lambda is too small, where the exact value of "too small" depends on the desired level &alpha of significance. Tests of the form "reject H0 if &Lambda < constant" are called likelihood-ratio tests; believe it or not, all of the tests we examined above are likelihood-ratio tests, or at least are based on approximations for &Lambda.

What do you say we do an example? Suppose we're testing H0:  &mu = &mu0 for a normal distribution with unknown mean &mu and known standard deviation &sigma. Based on a sample S = (x1, x2, ... xn), we know that &mu^ = x and that for any &mu,

L(&mu) = &Pii 1⁄√2&pi&sigma e&minus(xi−&mu)2⁄2&sigma2.

We can now calculate the likelihood ratio &Lambda = L(&mu0)⁄L(&mu^) as (I hope that I'm up to the HTML challenge...)

&Lambda   =
&Pii 1⁄√2&pi&sigma e&minus(xi−&mu0) 2⁄2&sigma2
&Pii 1⁄√2&pi&sigma e&minus(xi−x)2⁄2&sigma2

The numerator and denominator have the same number of factors of 1⁄√2&pi&sigma, so they go away. Recall that in the products, the exponents add, and then they subtract in the fraction. We can square out each of the numerators in the exponents to get

&Lambda = e &sum [(xi2 &minus 2xix + x2) ⁄2&sigma2 &minus (xi2 &minus 2xi&mu0 + &mu02)⁄2&sigma 2]

Notice that saying &Lambda is less than a constant is exactly equivalent to saying that the exponent in that last expression is less than a (different) constant, so we'll concentrate on the exponent. Since it's a common denominator, we'll concentrate for the moment on the numerator of the exponent. The xi2 terms cancel, and we end up with

&sum [x2 &minus &mu02 &minus 2xi(x &minus &mu0)] = &sum [(x + &mu0) (x &minus &mu0) - 2xi(x &minus &mu0)]

Since x and &mu0 are constant relative to the sum, we can factor out (x &minus &mu0) and get (x &minus &mu0) &sum [x + &mu0 &minus 2xi]. There are n terms, so the "constants" again come out of the sum, and we end up with (x &minus &mu0) (nx + n&mu0 &minus 2&sum xi. Since &sum xi = n(x (just think about the definition of x !!), the whole thing boils down to (x &minus &mu0) (nx + n&mu0 &minus 2nx) = (x &minus &mu0) (n&mu0 &minus nx) = &minusn(x &minus &mu0)2; the whole exponent in the &Lambda is therefore &minusn(x &minus &mu0)2⁄2&sigma2. This being less than a constant is equivalent to n(x &minus &mu0)2⁄2&sigma2 being greater than a constant, which is in turn equivalent to √n &sdot |x &minus &mu0|⁄√2&sigma being greater than a constant. Well, this makes sense, yes? First of all, it depends on how far apart x is from &mu0; &sigma serves as a yardstick, and the √n in the numerator reflects that the standard deviation of the sample mean decreases with the square root of the sample size, so the rest of the numerator had better get smaller when n gets larger. But we can do even better than that! Look: that last expression is equal to 1⁄√2 &sdot |x &minus &mu0|⁄(&sigma/√n). Since &sigma is known, under the assumption that H0 is true, the second factor is a standard normal variable. So in this case, we can explicitly calculate the critical value &mdash it's just 1⁄√2 times the appropriate critical value from a standard normal table.

That was lots of fun, yes? One great thing to know about our new toy &Lambda is that for any test of the form

H0:   &theta = &theta0
Ha:   &theta &ne &theta0

the statistic −2 log &Lambda has asymptotic null distribution &chi2, with the number of degrees of freedom equal to the number of (scalar) parameters in &theta. In other words, as the sample size n→∞, the distribution approaches a &chi2. This "asymptotic" business is always tricky, and I don't really have any catch-all rules of thumb to tell you how big is big enough; on the other hand, comparing a test statistic to the appropriate &chi2 critical value is a good place to start.

Recall the above example we worked out for a likelihood ratio test for the mean of a normal distribution with known standard deviation. The value of log &Lambda is the exponent   −(x &minus &mu0)2⁄2&sigma2, so   −2 log &Lambda = (x &minus &mu0)2⁄&sigma2. Since the distribution of (x &minus &mu0)⁄&sigma is (exactly!!) standard normal, and the definition of the &chi2 distribution with one degree of freedom is as that of the square of a standard normal variable, in that example −2 log &Lambda has the advertised &chi2 distribution no matter what the sample size is!

Likelihood-ratio tests are extremely flexible. The general form for a likelihood-ratio test statistic, which can be applied either with one sample or two, is

&Lambda =
max&theta∈H0 L(&theta)
max&theta∈H0∪Ha L(&theta)

(Actually, using "sup" for "supremum," or least upper bound, instead of "max" is more precise, because sometimes there's no max but rather an upper limit that you can get as close to as you want, but I think you get the idea.) Here's what that expression is trying to say: If the parameters you're interested in don't completely specify the distribution, then you may have some freedom within the null hypothesis, so you can maximize the likelihood over the choices you have; similarly, over all of the choices of parameters in the alternative hypothesis, choose the one maximizing the likelihood function. Generally, the alternative hypothesis is less restricted, so the likelihood you get in the denominator is always at least as large as that in the numerator. The asymptotic null distribution of −2 log &Lambda is again &chi², where the degrees of freedom are given by the difference in the number of free parameters between the null and alternative hypotheses.

As an example, suppose that you have a sample from a population that is known to have a normal distribution. If you wish to test the null hypothesis H0: &mu = &mu0, you would maximize the likelihood function in the numerator with &mu fixed at &mu0 but &sigma allowed to vary, and you would maximize the likelihood function in the denominator over all possible choices of &mu and &sigma. Since there are two free parameters in the denominator and only one in the numerator, the asymptotic null distribution of the test statistic −2 log &Lambda is therefore &chi² with 2−1=1 degree of freedom. If, on the other hand, you wanted to test H0: (&mu, &sigma) = (&mu0, &sigma0), then there is only one possible likelihood for the numerator, but the denominator is calculated as before. This time the number of free parameters in the numerator has gone down to 0, so the asymptotic null distribution of −2 log &Lambda is &chi² with two degrees of freedom.

As another example, suppose that we have two normal populations, where we assume that the standard deviations are known and equal, say &sigma, and we wish to test the hypothesis that the means are equal (H0: &mu1 = &mu2). Then we calculate three MLEs, all as we worked out above for normals with known σ, namely x1 for the first sample, x2 for the second sample, and xpooled for the two samples pooled together. The likelihood ratio then looks like

L(xpooled)⁄L(x1)L(x2),

where L(xpooled) is calculated with the combined samples, while L(x1) and L(x2) are calculated on their respective samples. (Note that the products in the numerator and denominator have the same number of factors, so they are on the same scale in some sense.) The appropriate number for the degrees of freedom is 1, since there is one free parameter in the top, namely the common mean, and there are two in the bottom, namely the two means for the samples taken separately.

Observe that the number of degrees of freedom would be precisely the same if we only assume that the variances are equal, rather than assuming that they are equal and known, because there is only one extra free parameter each in the numerator and denominator. The "exact" t-test based I gave you above, based on the assumption of equal variances, comes right out of the likelihood-ratio formula in this case. (The calculation isn't particularly sophisticated, although the manipulations you have to do are a bit messy to get into in this class.) Notice in particular that everything in sight can be calculated precisely assuming the null hypothesis; in particular, the statistic you get is independent of the population parameters. The only slightly tricky thing is to identify the right distribution as a t with n1 + n2 &minus 2 degrees of freedom.

On the other hand, if we don't assume the variances equal in the above example, then a likelihood-ratio-based test becomes problematic, because the null distribution of the statistic is impossible to calculate &mdash it would depend on how different the variances are. In other words, if the two means are equal and the variances are also equal, you'd get one distribution for &Lambda, but if the variances differed by a factor of 2, or 3, or 500, you'd get different distributions for &Lambda, so there's no one well-defined critical value you can use for comparison with your test statistic. This is what caused Fisher to suggest the above non-equal-variances test, which, I repeat, can only be guaranteed to provide a significance level at or less than the desired one.

As yet another example, the hypothesis that the two means are equal and the two variances are equal, against the alternative that there is some difference either in mean or variance, is a straightforward test to carry out, at least for large samples, because again the null distribution does not depend on the specific parameters. In this case, the numerator of the likelihood ratio has two free parameters, namely the common mean and the common variance, while the denominator has four, namely the mean and variance in each sample; thus, the asymptotic null distribution of −2 log &Lambda is &chi² with 2 degrees of freedom.

Now, here's the payoff for our situation: We can now construct a test, based on the likelihood ratio, to tell two typists apart. How would it go? Well, you could reason something like this: If two samples were typed by the same person, the distributions should be identical for all letter pairs in the two samples. So take all the letter pairs that appear more than some minimum number of times (maybe 5); suppose there are k such pairs. Then form the joint likelihood ratio based on all the letter pairs. For each pair, there are two free parameters in the numerator and four in the denominator, just like in the preceding paragraph, so the null distribution for our test statistic −2 log &Lambda is asymptotically &chi² with 2k degrees of freedom. Or one could adopt the assumption that variances are equal in each pair; this certainly ought to be true under the null hypothesis, anyway. In that case, the &chi² has k degrees of freedom. The disadvantage is that the assumption of equal variance reduces the power of the test, but then it's less sensitive to outliers and deviations from normality.

Practical Considerations: Lessons We Have Learned

All that said, we would like to share with you some wisdom, acquired through the bitter experience of trial and error, that will almost doubtless be of some use to you. There are a number of reasons, many of them based on harsh realities about the nature of Reality itself, why the above method doesn't work quite as well as you're really rooting for it to.

The first of these reasons is that whole pesky "asymptotic" thing I mentioned above and then proceeded to sweep under the rug. The fact is that 5 is not a large number, so if you use samples down to size 5, it's a fair bet that the asymptotics of that sample's contribution to the test statistic have not settled down on their asymptotic value. Years ago, statisticians much brighter and more motivated than Yours Truly would have labored to find an analytic description for the small-sample distribution of &Lambda or of −2 log &Lambda, and I'm not sure whether they would have succeeded. However, in this technological age, there is actually a beautiful and simple remedy to our difficulty. Use our good friend Monte Carlo, with whom we were introduced back in that more innocent time when we were interested in guns. Details? Well, recall that we're assuming that the distribution of keystroke-pair timings are normal, and the null hypothesis states that the means and variances are equal. Since the distribution of −2 log &Lambda doesn't depend on the mean or the variance, we can just take standard normals of the appropriate sizes for all the keystroke pairs and both typists, draw from these distributions randomly, calculate −2 log &Lambda, and repeat a bunch of times to find critical values. Then we calculate −2 log &Lambda for our data and compare it to whatever critical value we deem appropriate.

The second difficulty with the method outlined above is in the nature of the data. We found that the data generally aren't exactly normally distributed. Often, but not always, the distribution of the data is approximately lognormal, meaning that the logarithms of the values are approximately normal, in each bin. So one thing that one might try in order to make the test work better would be to apply a log-transform to all the data up front. In addition to being non-normal, the data are fraught with outliers, values that don't seem to fall into the distribution well. It's not hard to see how outliers might occur: The typist may have become confused in the middle of a word about spelling; they may have had to scratch their head or become distracted in some other way. On the other hand, maybe the outliers are just part of a typist's "usual" habits! I personally believe that the latter is probably true, but if we're trying to model the data with relatively simple models such as normal or lognormal distributions, they just aren't sophisticated enough to handle these intermittent phenomena, so we're probably better off throwing them out. Tukey suggested the following heuristic for determining whether or not something is an outlier: Calculate the interquartile range, which is the 75th percentile minus the 25th percentile; if a data value lies more than 1.5 times this quantity either above the 75th percentile or below the 25th percentile, it's an outlier.

I should also mention here that we're surely not constrained by normals and lognormals! Any distribution for which we have a chance of calculating MLEs is a valid candidate. I might suggest trying exponential distributions; for the adventurous, the Weibull might be fun as well! In the latter case, you'll need to optimize the likelihood function with numerical methods, but heck, we learned about those back when we were fighting snipers.

Yet another issue seems to be that of selecting the appropriate number of keystroke pairs to use in one's evaluations. It seems the most logical to consider only those keystroke pairs that occur at least as many times as some cutoff value. What should that cutoff be? On the one hand, setting it low allows us to use more data, but on the other hand, small samples can have distributions very different from their underlying population and can reduce the power of your test. This is a parameter with which you may need to experiment.

Resumé of Methods

Below are some methods we have tried and some we haven't. It may be possible to use some of these approaches in combination.

*⁄** *

*⁄** *